A Quadratic Programming Approach to Manipulation in Real-Time

Manipulation tasks usually involve the control of redundant robots to reach large workspaces while avoiding obstacles and satisfying other constraints. This results in motion planning in high-dimensional space. In addition, whole-body manipulation tasks using multi-limbed robots may need the control of more than one manipulators. Modular robots can be used to construct many useful morphologies with multiple chains for manipulation tasks. Multiple chains can behave as a gripper to grasp some objects although their geometry shapes can be very simple. A significant feature for these morphologies built by many modules is that the motion of chains are usually strongly coupled, namely these chains usually share many degrees of freedom. Also a general modeling solution is necessary since the a set of modules can form a large number of morphologies. We present a real-time planner to handle manipulation planning tasks including a kinematics modeling solution for arbitrary morphologies, a real-time controller to handle multiple motion tasks even if they are coupled, and a novel obstacle avoidance strategy based on a obstacle approximation method. This planner is demonstrated on real modular robots.

In a modular robotic system, a module can be modeled as a graph with all kinematics information embedded. For example, a SMORES-EP module is shown below that has four degrees of freedom and four connectors. A module graph can be generated to describe the kinematics model of this module where each vertex is a rigid body in the module (a connector or the module body) and each edge represents how adjacent rigid bodies are connected. A morphology is constructed by several modules and we can obtain the kinematics graph for a given morphology by composing the module graphs through connecting connector vertices. Then a kinematic chain from one frame to another frame is simply derived by following the shortest path between these two frames and a kinematics model for this chain can also be generated easily. More details can be found in the referenced papers.

Given a kinematic chain and a control task, a position control law can be built. It is shown that when there are multiple control tasks, e.g. moving multiple rigid bodies at the same time, we can simply stack the control law for each task even if some motion tasks are coupled, namely some kinematic chains can share some degrees of freedom. For a redundant robotic system, this control problem can be formulated as a quadratic program in which the control laws for all motion tasks are linear constraints. The hardware constraints, including position and velocity limits, can also be added as inequality constraints. A hardware demonstration is shown using CKBot modules.

During the task, modules cannot move beyond the workspace boundary and collide with any environment obstacles. Modules are usually in regular shapes, such as spheres or cubes, and we use a sphere to approximate the geometry size of a module. The workspace can be defined as a polyhedron and for each facet of the polyhedron, a linear constraint can be built to keep the module from traversing the boundary. Obstacles can be approximated by a sphere-tree construction algorithm and we can form a virtual plane between the module and every obstacle sphere so that a similar linear constraint can be built to avoid collision. There can be a very large number of obstacle spheres and the constrained manifold makes the optimization problem difficult to solve. However, these obstacle spheres can be pruned significantly as we build these virtual planes, and this process can be executed efficiently by iteratively applying an erase-remove idiom technique for real-time applications.

 

 

 

 

 

 

 

 

 

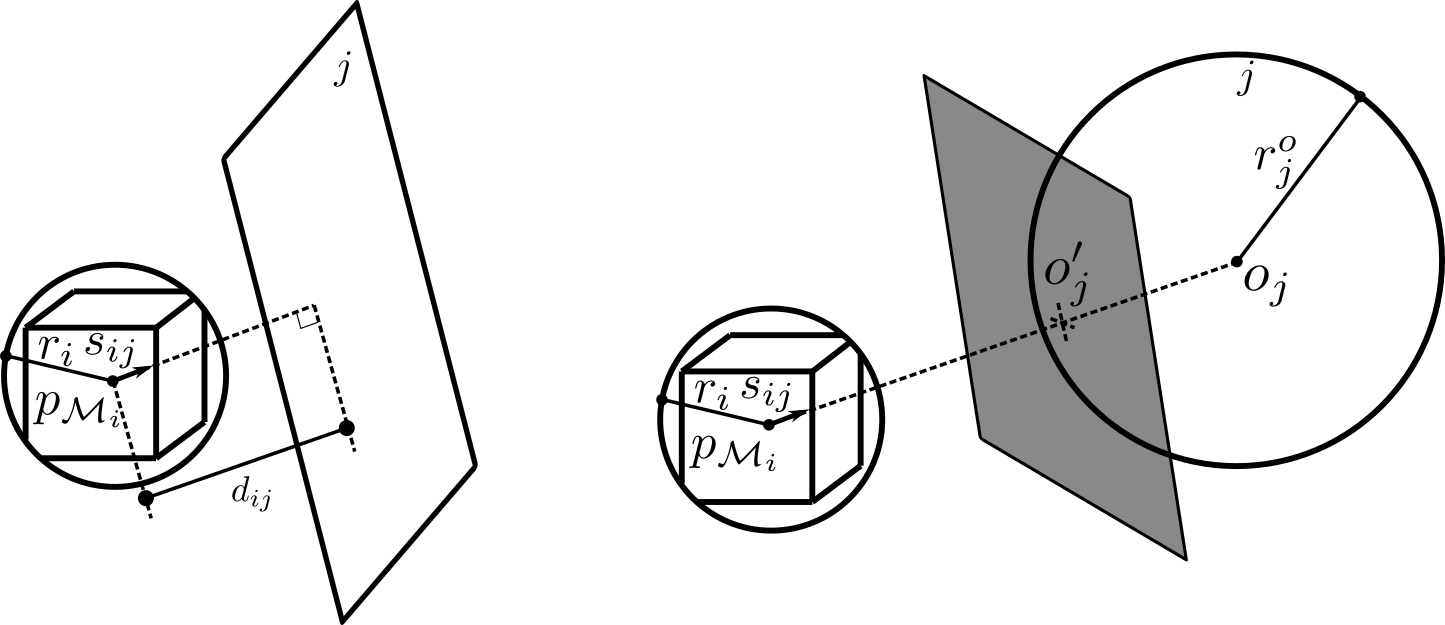
The control and motion planning task can be formulated as a sequential optimization process. The control law is embedded as a term in the objective function. In the process, if any module is close to some obstacle sphere, we add a term to the objective function to penalize the motion of this module towards to that obstacle. If any module makes contact with some obstacle sphere, this module will be forced to move away by defining a repulsive velocity as the normal to the corresponding obstacle virtual plane that can be done by adding a hard inequality constraint and remove the previously added penalizing term for this module from the objective function. Several experiments are shown in the following video.

Publications

Note: The Obstacle Avoidance model in the published IRC paper from IEEE Xplore is not correct, and the correction is shown in the following provided PDF file.

• C. Liu and M. Yim, “A quadratic programming approach to modular robot control and motion planning,” in 2020 fourth ieee international conference on robotic computing (irc), Taichung, Taiwan, 2020, pp. 1-8.
  [Bibtex]

  @INPROCEEDINGS{CL:MY:20,
  author = {C. {Liu} and M. {Yim}},
  booktitle = {2020 Fourth IEEE International Conference on Robotic Computing (IRC)},
  title = {A Quadratic Programming Approach to Modular Robot Control and Motion Planning},
  year = {2020},
  volume = {},
  number = {},
  pages = {1-8},
  doi = {10.1109/IRC.2020.00008},
  month = {Nov},
  address = {Taichung, Taiwan},
  pdf = {https://www.modlabupenn.org/wp-content/uploads/2021/07/Liu_irc_2020.pdf}
  }

• C. Liu and M. Yim, “A quadratic programming approach to manipulation in real-time using modular robots,” The international journal of robotic computing (invited), vol. 3, iss. 1, pp. 121-145, 2021.
  [Bibtex]

  @ARTICLE{CL:MY:21,
  author = {Chao {Liu} and Mark {Yim}},
  journal = {The International Journal of Robotic Computing (Invited)},
  title = {A Quadratic Programming Approach to Manipulation in Real-Time Using Modular Robots},
  year = 2021,
  volume = 3,
  number = 1,
  pages = {121-145},
  doi = {10.35708/RC1870-126268},
  pdf = {https://www.modlabupenn.org/wp-content/uploads/2021/08/Liu_ijrc_2021.pdf}
  }