Finding Structure Configurations for Flying Modular Robots

Flying Modular Structures offer a versatile mechanism that can change the arrangement of constituent actuators according to task requirements. In this work, we extend a modular aerial platform that can expand its actuation capabilities depending on the configuration. Each module is composed of a quadrotor in a cage that can rigidly connect with other modules. The quadrotor is connected with the cage by a revolute joint that allows it to rotate with respect to the cage. Modules located in the structure are either parallel or perpendicular to one another. The task specification defines forces and moments needed during the execution. We propose two search methods to find a configuration that can satisfy the specification. The first approach consists of an exhaustive search that yields optimal structure configurations by exploring the whole search space. The second approach proposes a heuristic based on subgroup search, reducing the problem complexity from exponential to linear. We validate our proposed algorithms with several simulations. Our results show that the proposed heuristic is computationally efficient and finds a near-optimal configuration even for flying modular structures composed of a large number of modules.

Module Configuration Search

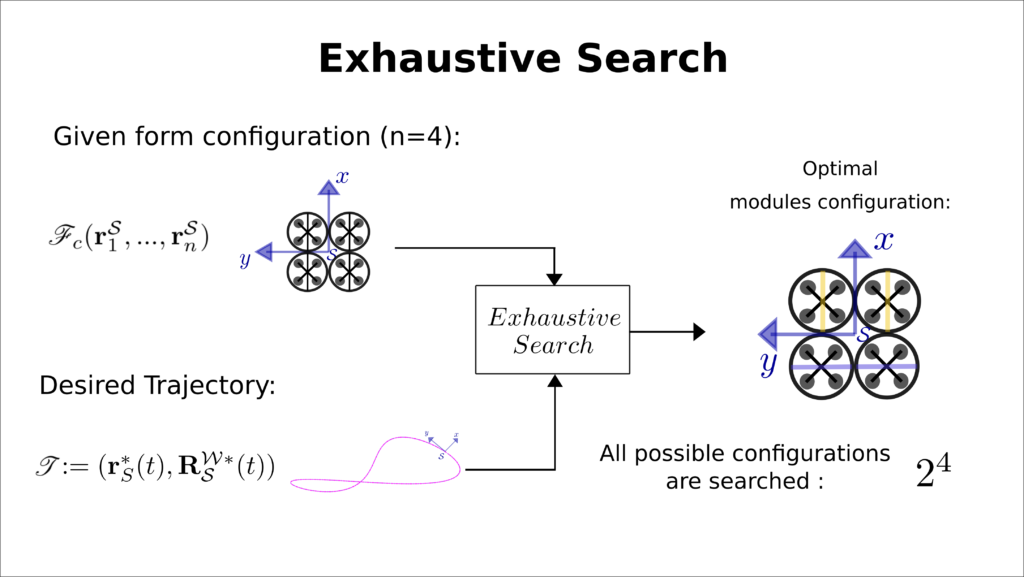
We propose to find optimal and near-optimal structure configurations for a given path and number of modules. More specifically we introduce a module configuration search that minimizes control effort along a predefined trajectory and a pre-defined form configuration. For a baseline, we developed an algorithm that finds optimal solutions by exploring all possible combinations in the search space. This Exhaustive Search checks all module configuration combinations, and has complexity exponential in n. In scenarios for which n is large and multiple changes in the form configuration and trajectory are required, a faster method to compute module configurations is desirable. We propose a greedy approach that is near-optimal, but computationally efficient, called SubGroup Search. It first uses divide the structure into layers and create subgroups within each layer and according to the module’s Euclidean distance to the structure’s frame. Using this approach, the search applies to each subgroup instead of the whole structure search space, thus decreasing substantially the module configuration space to be explored.

 

Conclusions

In this work a configuration generalization of the system presented in ModQuad-DoF  is introduced. A flying structure controller that takes as inputs trajectories in SE(3) was presented along two configuration optimization search methods. We demonstrated through simulation results that the Exhaustive Search yields optimal module configurations utilizing a costly search method whereas the SubGroup Search yields near-optimal results though the configuration space to be explored was substantially reduced. The results obtained from the proposed search method shows an important contribution for computing configurations for flying modular structures composed of a large number of modules. In future work, we aim to extend this study to the form configuration level of the structure. Optimization of both module and form configuration would allow us to design flying modular robots capable to perform a diverse range of tasks by self-reconfiguration. Furthermore, we plan to add constraints to our controller to handle scenarios in which forces that keeps modules docked together are limited.

Publications

• B. Gabrich, D. Saldana, and M. Yim, “Finding structure configurations for flying modular robots,” in Ieee/rsj international conference on intelligent robots and systems 2021, to be presented, Czech Republic, Prague, 2021.
  [Bibtex]

  @inproceedings{BG:DS:MY:21,
  title = {Finding Structure Configurations for Flying Modular Robots},
  author = {Gabrich, Bruno and Saldana, David and Yim, Mark},
  booktitle = {IEEE/RSJ International Conference on Intelligent Robots and Systems 2021, to be presented},
  address = {Czech Republic, Prague},
  year = {2021},
  pdf={https://www.modlabupenn.org/wp-content/uploads/2021/08/iros2021_brunogabrich_modlab.pdf}
  }